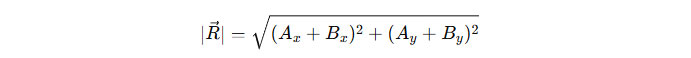
Vektor adalah salah satu konsep dasar dalam matematika dan fisika yang sangat penting, terutama ketika kita berbicara tentang pergerakan, gaya, atau perubahan posisi. Menurut vectorsection.org, vektor tidak hanya sekadar ukuran atau besaran, tetapi juga melibatkan arah, sehingga memerlukan operasi tertentu untuk menjumlahkan, mengurangkan, atau mengalikan vektor. Dalam artikel ini, kita akan membahas berbagai rumus operasi vektor, mulai dari penjumlahan, pengurangan, hingga perkalian, beserta contoh penerapannya.
Penjumlahan Vektor
Penjumlahan vektor adalah operasi yang dilakukan untuk menggabungkan dua atau lebih vektor menjadi satu vektor hasil. Penjumlahan vektor ini dilakukan dengan memperhatikan baik besar maupun arah vektor. Ada dua metode yang umum digunakan untuk menjumlahkan vektor: metode grafis dan metode analitis.
1. Metode Grafis
Dalam metode grafis, vektor-vektor yang akan dijumlahkan digambarkan dalam bentuk garis yang diwakili oleh panah. Vektor pertama digambar terlebih dahulu, lalu vektor kedua digambar dari ujung vektor pertama. Vektor hasil penjumlahan adalah garis yang menghubungkan titik awal vektor pertama dengan ujung vektor kedua.
2. Metode Analitis
Untuk metode analitis, kita biasanya memecah vektor menjadi komponen-komponen pada sumbu X dan Y. Misalnya, jika ada dua vektor A dan B, yang masing-masing memiliki komponen-komponen (Ax, Ay) dan (Bx, By), maka penjumlahan vektor A dan B secara analitis dapat ditulis sebagai:
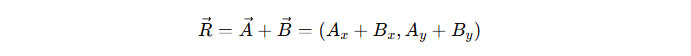
Setelah itu, hasil penjumlahan komponen-komponen tersebut akan memberi komponen-komponen baru pada sumbu X dan Y, yang kemudian dapat dihitung panjangnya menggunakan rumus Pythagoras jika diperlukan:
Contoh: Misalkan vektor A = (3, 4) dan vektor B = (1, 2). Penjumlahan kedua vektor ini menghasilkan vektor R:
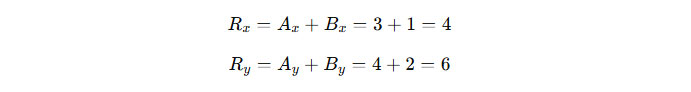
Sehingga, vektor hasil penjumlahannya adalah R = (4, 6).
Pengurangan Vektor
Pengurangan vektor mirip dengan penjumlahan vektor, namun dengan arah yang berlawanan. Untuk mengurangi vektor A dengan vektor B, kita cukup menambah vektor A dengan vektor negatif B. Vektor negatif B adalah vektor dengan panjang yang sama dengan vektor B, tetapi arahnya berlawanan.
Secara analitis, rumus pengurangan vektor A – B adalah:
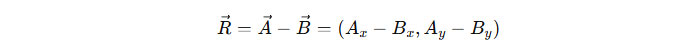
Seperti penjumlahan, kita bisa menghitung panjang vektor hasil pengurangan dengan rumus Pythagoras:
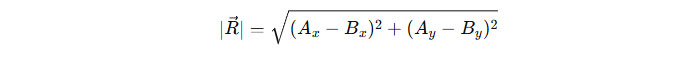
Contoh: Misalkan vektor A = (4, 5) dan vektor B = (2, 3). Pengurangan vektor A dengan B menghasilkan vektor R:
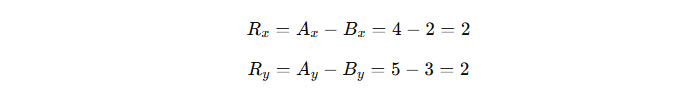
Maka, hasil pengurangan vektor adalah R = (2, 2).
Perkalian Vektor
Ada dua jenis perkalian vektor yang sering digunakan dalam matematika dan fisika, yaitu perkalian skalar (dot product) dan perkalian silang (cross product).
1. Perkalian Skalar (Dot Product)
Perkalian skalar atau dot product adalah operasi perkalian antara dua vektor yang menghasilkan nilai skalar (angka). Rumus perkalian skalar antara dua vektor A dan B dengan komponen-komponen Ax,AyA_x, A_y dan Bx,ByB_x, B_y adalah:
![]()
Hasil dari perkalian skalar adalah angka (skalar), dan tidak memiliki arah. Perkalian skalar ini sering digunakan untuk menghitung besarnya gaya yang bekerja dalam arah tertentu, seperti ketika kita menghitung pekerjaan yang dilakukan oleh gaya.
Contoh: Misalkan vektor A = (2, 3) dan vektor B = (4, 1). Perkalian skalar A dan B adalah:
![]()
Jadi, hasil perkalian skalar kedua vektor tersebut adalah 11.
2. Perkalian Silang (Cross Product)
Perkalian silang atau cross product adalah operasi perkalian antara dua vektor yang menghasilkan vektor baru yang tegak lurus terhadap kedua vektor yang dikalikan. Perkalian silang biasanya digunakan dalam perhitungan gaya, momen, atau medan magnet.
Rumus perkalian silang antara dua vektor A dan B dalam ruang tiga dimensi (dengan komponen Ax,Ay,AzA_x, A_y, A_z dan Bx,By,BzB_x, B_y, B_z) adalah:
![]()
Hasil dari perkalian silang adalah sebuah vektor yang memiliki arah tegak lurus terhadap kedua vektor yang dikalikan. Besarnya vektor hasil perkalian silang ini dapat dihitung dengan rumus:
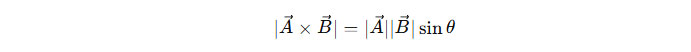
di mana θ adalah sudut antara kedua vektor A dan B.
Contoh: Misalkan vektor A = (1, 2, 3) dan vektor B = (4, 5, 6). Perkalian silang A dan B adalah:
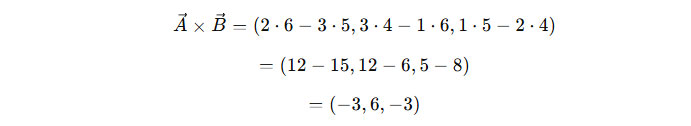
Jadi, hasil perkalian silang kedua vektor tersebut adalah vektor (-3, 6, -3).
Kesimpulan
Operasi vektor seperti penjumlahan, pengurangan, dan perkalian adalah dasar penting untuk memahami banyak fenomena dalam fisika dan matematika. Penjumlahan vektor digunakan untuk menggambarkan total resultan dari beberapa vektor yang saling berinteraksi, sementara pengurangan vektor berguna untuk menemukan perbedaan antara dua vektor yang merepresentasikan arah dan besar yang berbeda. Perkalian vektor, baik perkalian skalar (dot product) maupun perkalian silang (cross product), memiliki aplikasi yang sangat luas, misalnya dalam perhitungan kerja dalam fisika atau menentukan arah gaya dalam interaksi antar partikel. Setiap operasi ini memiliki rumus tertentu yang harus dipahami dengan baik agar bisa diterapkan dengan tepat dalam berbagai konteks masalah.
Dengan memahami rumus-rumus ini, kamu bisa menganalisis gerakan, gaya, atau interaksi antara objek di dunia nyata dengan lebih mudah dan akurat. Sebagai contoh, dalam fisika, vektor digunakan untuk menjelaskan gerak benda, termasuk percepatan, kecepatan, dan gaya yang bekerja padanya. Di dunia teknik dan rekayasa, operasi vektor juga sangat penting dalam perancangan sistem mekanik dan struktur. Tanpa pemahaman yang solid tentang operasi-operasi vektor, sulit untuk menyelesaikan masalah yang melibatkan banyak variabel dalam ruang tiga dimensi, yang sering kali muncul dalam berbagai aplikasi ilmiah dan teknik.